Antwort zur Frage 12

Ich möchte die Antwort mit einem didaktischer Zugang geben. Das nachstehende Bild dazu finden Sie in Referenz [7] (W. Send, Aerodynamik des Tierflugs, MNU 47/3 (1994), 131-142) meines Artikels. Ich möchte den wesentlichen Gehalt des Textes zu dem Bild hier wiederholen, ergänzt um einige Aspekte, die sich aus Diskussionen mit Kollegen in meinem Institut ergeben haben. Das Bild aus dem MNU-Artikel ist hier noch einmal in besserer Auflösung vorhanden.

   Die Gegenkraft zum Auftrieb findet sich wieder als Druckänderung im Unendlichen, nicht als Reaktionskraft zu abgelenkten Fluidpartikeln. Der Unterdruck auf der Oberseite verteilt sich mit zunehmender Entfernung ebenso über einen immer größeren Bereich des Fluids oberhalb der Tragfläche, wie es der Überdruck auf der Unterseite tut. Man kann es so sagen: Mit der Oberseite "saugt" sich das Profil im Fluid nach oben an, mit seiner Unterseite stützt sich das Profil nach unten im Fluid ab. Diese beiden Anteile der Gegenkraft sind aber unendlich entfernt. Das Profil würde also durch die Wirkung des Auftriebs sofort nach "oben" beschleunigt, wenn es nicht durch eine weitere - an dieser Argumentation gar nicht beteiligte - Haltekraft zu seiner stationären Bewegung gezwungen würde (dies kann z.B. die Schwerkraft über das passende Eigengewicht sein oder eine andere unsichtbare Fixierung). Diese Argumentation gilt in Strenge nur für ein unendlich ausgedehntes Fluid.

Man muss sich klar machen, dass die Gegenkraft zum Auftrieb entweder durch diese Druckänderung im Unendlichen, oder aber durch die Reaktionskraft abgelenkter Partikel ausgeglichen werden kann, aber nicht durch beide Gründe gleichzeitig. Die Argumentation mit der Partikelablenkung findet sich in vielen Physikbüchern, ohne dass sie wirklich bewiesen wird. Dabei wird dann der gleichzeitig vorhandenen Druckänderung aber gar keine Aufmerksamkeit mehr geschenkt.

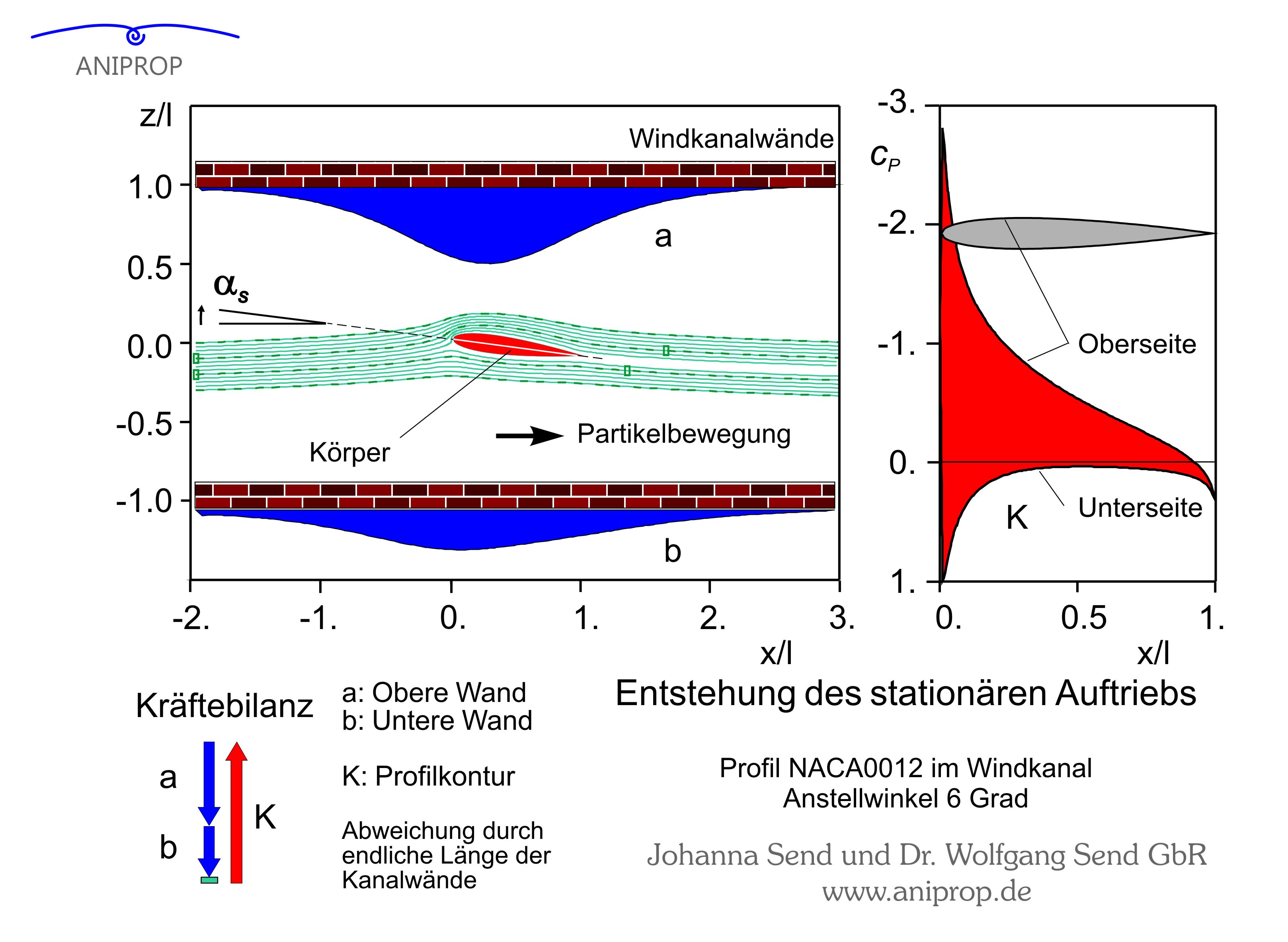
Wie kann man diesen Nachweis der Druckänderung anschaulich führen? Dazu betrachten wir ein Profil, dem in einem gewissen Abstand zwei zur Anströmung parallele Wände zugefügt sind, wie sie die Zeichnung zeigt. Diese Wände bewegen sich mit dem Profil mit. Es gibt also - was die Bezeichnung "Windkanalwände" verschweigt - auch eine Außenströmung zu diesen Wänden. Zwischen den Wänden unterscheidet sich die Anordnung aber nicht von einem gewöhnlichen Windkanal. Wir können nun die Druckverteilung auf diesen mitbewegten Wänden berechnen. Die Verteilung des Differenzdrucks ist als blaue Kurve für beide Wände in der Zeichnung dargestellt. Bei der Tragfläche in der rechten Bildhälfte ist es nicht anders, nur dass die Druckverteilung auf Ober- und Unterseite noch getrennt dargestellt ist und nicht bereits die Druckdifferenz. Die Summierung der Druckdifferenz führt zur Auftriebskraft*), die als roter Pfeil links unten im Bild aufgetragen ist. Auch die Druckdifferenzen auf den beiden Wänden führen zu zwei Kräften, die maßstabsgerecht neben dem Auftrieb dargestellt sind. Bis auf das kleine grüne Rechteck, das den Fehler in der Rechnung durch endlich lange Kanalwände zeigt, gleichen die beiden Kräfte an den Wänden den Auftrieb genau aus. An einer Reaktionskraft aus abgelenkten Partikeln ist kein Bedarf mehr.

Grenzübergang. Wir stellen uns nun vor, dass diese beiden Wände immer weiter vom Profil entfernt und zugleich zu beiden Seiten immer mehr verlängert werden.  Dabei verteilen sich die beiden Kräfte über eine immer größere Fläche und die Druckunterschiede auf den beiden Wänden werden immer kleiner, aber die Gegenkräfte auf Ober- und Unterseite bleiben erhalten. Leider lässt sich dieser Grenzübergang mit einem normalen Rechenprogramm nicht ohne Weiteres nachvollziehen. Aber das Newtonsche Prinzip actio=reactio gilt auch für den Auftrieb.

Anmerkung zum  3D Fall. Die voranstehende Argumentation gilt auch für die Tragfläche endlicher Spannweite mit Randwirbeln. Der Auftrieb entsteht hier nicht etwa als Gegenkraft zu den absinkenden Randwirbeln. Die Tatsache, dass die Wirbelschleppe hinter dem Flugzeug "nach unten" sinkt, hat damit zu tun, wie die beiden Randwirbel hinter dem Flugzeug miteinander in Wechselwirkung treten. Sie ziehen sich nicht nur an, weil sich zwischen ihnen ein Unterdruck aufbaut, sondern sie drücken sich auch gegenseitig nach unten, weil der eine Wirbel sich im induzierten Geschwindigkeitsfeld des anderen aufhält. Man erhält den richtigen Auftrieb mit geringen Abweichungen auch aus Rechnungen, in denen das Absacken der beiden Wirbel gar nicht berücksichtigt ist. Im Übrigen wird der Auftrieb gerade dann größer, wenn die Randwirbel gleich bleiben und nur die Tragfläche in Spannweite verlängert wird. In der Mitte der Tragfläche (z.B. bei einem  Segelflugzeug) unterscheiden sich die Strömungsverhältnisse kaum mehr vom  2D Fall.

*) Gegenüber der Tragfläche ohne begleitende Wände unterscheidet sich der Auftrieb nur unwesentlich. Zu Zahlen siehe auch die MNU-Publikation.