Antwort zur Frage 13

Zunächst zum zweiten Teil Ihrer Nachfrage. Die Antwort ist eindeutig: Auf jeder Kontrollfläche, die das Profil in Abb. 5 umschließt, findet sich die Gegenkraft ebenfalls wieder. Das verlangt der Impulssatz, und die numerische Nachprüfung ergibt auch mit guter Genauigkeit den Auftriebsbeiwert, der für das Profil berechnet worden ist. Dazu habe ich weiter unten noch einige Ergänzungen angefügt.

Sie haben Recht, wenn Sie feststellen, dass das Bild mit den Wänden oberhalb und unterhalb des Profils etwas Anderes ist als allein das Profil. Als ich das Bild 1994 für die MNU-Zeitschrift angefertigt habe, hatte ich folgende Motivation: Wie kann man zeigen, dass ein Profil Auftrieb erfährt, ohne dass die Stromlinien - wie in vielen Physikbüchern in willkürlicher Weise gezeichnet - hinter dem Profil nach unten abbiegen. Diese Darstellungen, die im Hinblick auf die Begründung des Auftriebs im 2D Fall falsch sind, sollen zeigen, dass die Fluidpartikel eine Ablenkung erfahren, deren Reaktionskraft den Auftrieb hervorruft. Die Wände sind ja nichts Anderes als Teil einer solchen Kontrollfläche, deren Ränder aber erzwungenermaßen zugleich Stromlinien sind. Das Profil erfährt seinen Auftrieb, die Gegenkraft findet sich - bis auf geringe Abweichungen durch die endliche Länge der Wände - in Form von zwei Druckverteilungen  an den Wänden wieder. Die Einführung der Wände soll vermeiden, den Begriff der Kontrollfläche überhaupt diskutieren zu müssen.

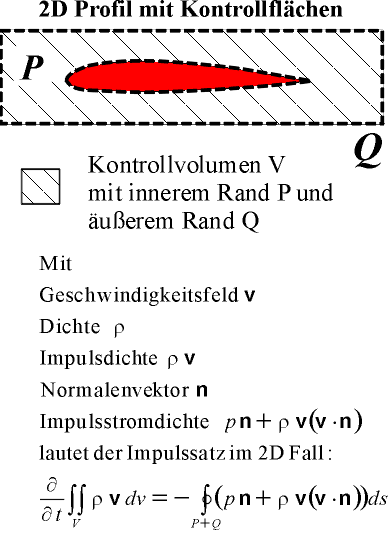
Ergänzung: Nebenstehend ist der Impulssatz für den 2D Fall und mit der Annahme angegeben, dass keine Zähigkeit im Fluid vorhanden ist (also der im Artikel betrachtete Fall der infinitesimal dünnen Grenzschicht). Im 3D Fall ist das linke Integral ein Volumenintegral und das rechte ein Oberflächenintegral. Im 2D Fall wird links über eine Fläche, rechts über eine geschlossene Kurve integriert. v ist das Geschwindigkeitsfeld der Relativbewegung der Partikel, wie sie der mitbewegte Beobachter sieht. n ist der Normalenvektor der jeweiligen Oberfläche, der aus dem Volumen heraus zeigt. Zeigt n genau in Bahnrichtung eines Partikels, dann  ist die Dichte des Impulsstroms in diese Richtung gerade p+rho v². Die Größe kann man folgendermaßen verstehen: Hält man "in Gedanken" eine kleine Fläche F quer in diesen Strahl, so dass dieser zur Seite spritzt, dann ist die Kraft auf die Fläche gerade  rho v² F. Dabei ist gleicher Druck vor und hinter der Probefläche unterstellt. Senkrecht dazu ist die Impulsstromdichte nur p; eine so orientierte Fläche muss also nur den Druck aushalten. Die Dichte des Impulsstroms in Bahnrichtung darf man nicht verwechseln mit dem Staudruck  p+1/2 rho v².
Die zeitliche Änderung der Impulsdichte über das "Volumen" V ist gleich dem Impulstrom über die Oberfläche des Volumens: Eine Impulsänderung der im Volumen vorhandenen Masse entsteht durch die auf die Oberfläche einwirkende Kraft. Das Volumen V hat als inneren Rand die Oberfläche P des Profils und als äußeren Rand die Fläche Q, die willkürlich gewählt sein kann. Da die Strömung stationär ist, gibt es keine zeitliche Änderung des Gesamtimpulses von V, und der rechte Ausdruck muss verschwinden. Diese Tatsache kann genutzt werden, um die Kräfte am inneren Rand aus den Kräften am äußeren Rand zu berechnen. Am inneren Rand ist der Ausdruck v*n gleich null, denn das ist gerade die Bedingung für die tangentiale Umströmung der Profiloberfläche. Das Integral über die Fläche P ergibt Widerstand und Auftrieb.
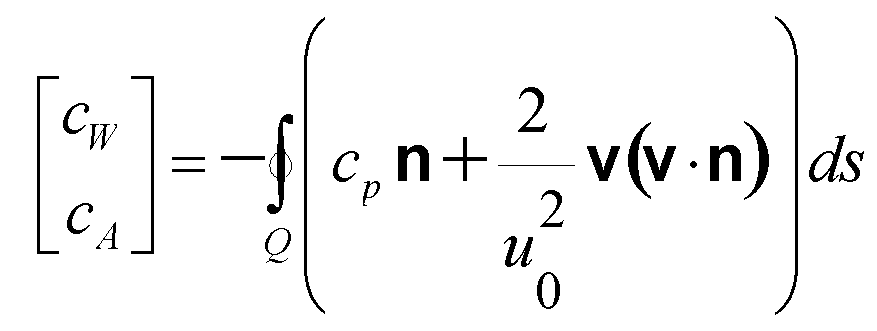Da das rechte Integral durch Hinzufügen einer Konstanten im Integranden seinen Wert nicht ändert, kann man es auf die Beiwerte für Auftrieb und Widerstand umschreiben. Dazu wird entsprechend der Definition des Druckbeiwerts vom Druck p der Ruhedruck im Fluid abgezogen und der ganze Integrand sodann durch 1/2 rho u₀² geteilt. Der Anteil über den inneren Rand ergibt Widerstands- und Auftriebsbeiwert. Der Anteil über den äußeren Rand Q steht auf der rechten Seite und kann errechnet oder aus Messungen näherungseise ermittelt werden. Der Nutzen des Integrals zeigt sich bei geschickter Auswahl der Kontrollflächen. Eine wichtige Anwendung ist z.B. die Bestimmung des Widerstands eines Profils im Windkanal aus der sogenannten Nachlaufdelle (mit den Partikeln, die dicht an der Oberfläche mitgerissen worden sind).
Zu der Lösung in Abb. 5 des Artikels Physik des Fliegens ist eine Auswertung des Impulssatzes angegeben für eine Rechteckfläche um das Profil NACA2312. Eine Erläuterung der Bezeichnungen ist ebenfalls beigefügt. Es sei angemerkt, dass die Anteile im rechts stehenden Integral des Impulssatzes je nach Lage der Kontrollflächen sehr unterschiedliche Beiträge liefern. Für die Auswertung ist eine Kontrollfläche gewählt, die dem oben erwähnten Beispiel in der MNU-Arbeit nahe kommt. Die Flächen in Stromrichtung sind lang und parallel zur Anströmung.